ラザフォード後方散乱分光法(RBS)
1.はじめに
ラザフォード後方散乱分光法は、固体表面近傍(最表面より約1>μm)の元素組成の深さ方向分布を直接測定する有力な手法である。後方散乱によって失うエネルギーより衝突相手の元素を同定でき、固体媒質電子との相互作用によって失うエネルギー量より散乱の起こった場所の深さを知ることができる。固体が単結晶の場合は、チャネリングとブロッキング効果を利用することによって原子配列の情報を取り出すことも可能である。keV-MeVの高速イオンは古典的粒子としてみなすことができ、固体媒質中を走るイオンに対しては明確な軌道の概念を使うことができる。この点が、波動としての回折効果によって原子配列の情報を引き出す電子や光ビーム分析と大きく異なっている。
測定した後方散乱スペクトルより詳細な定量的情報を引き出すためには、計算機シミュレーションがしばしば必要となる。試料構造を規定するパラメータを仮定することによって後方散乱スペクトルを構成し、実スペクトルにベストフィットさせることによって構造を決定することができる。後方散乱スペクトルを構成するためには、解析的方法とモンテカルロ法の2通りの方法がある。元素性分布や欠陥分布、膜成長初期過程のアイランド構造(アイランドの平均厚さ、その揺らぎ、占有率)など平均的分布を決めるのに適している。一方、モンテカルロ法は表面や界面の原子配列の決定に威力を発揮する。まず、最初に各原子に対して近接衝突(Close-Encounter)確率を計算し、これより後方散乱スペクトルを構成するという手順をとる。
ここでは、解析的手法による計算機シミュレーションについて説明を行う。まず最初にラザフォード後方散乱分光法の概念について説明する。次に後方散乱における物理的な基礎と計算機シミュレーションの手順について説明し、最後に実験結果とシミュレーションによる解析結果について述べる。
2. ラザフォード後方散乱分光法の概念
2-1. 測定装置
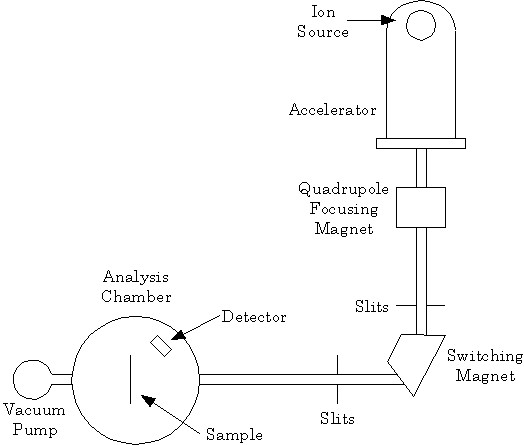
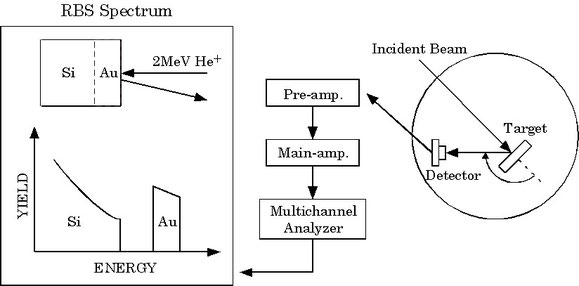
3. ラザフォード後方散乱の物理的基礎
3-1. カイネティック因子(Kinematic Factor)

3-2. 散乱断面積
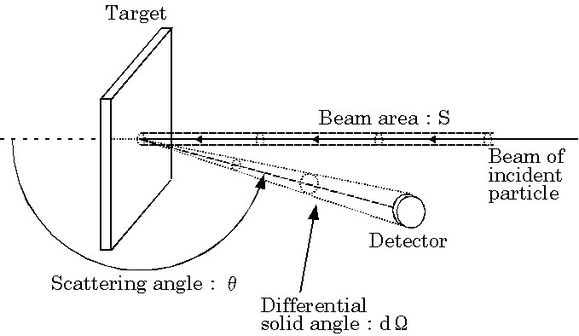
3-3. エネルギー損失と阻止断面積
3-4. エネルギー・ストラグリング


3-4. 出射エネルギーの計算
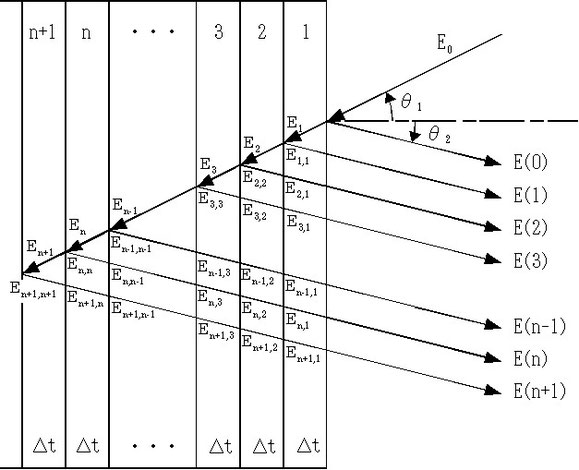
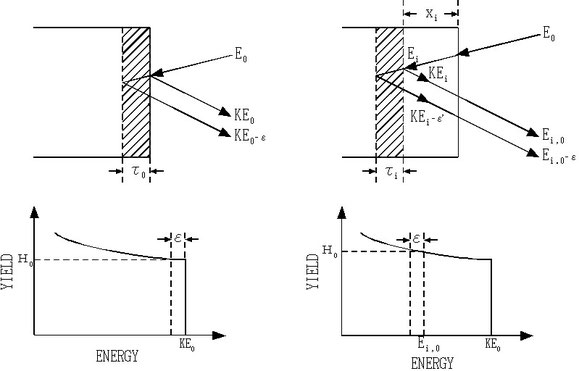
4. 実際の測定スペクトル

シミュレーションによるスペクトル解析
参考文献
- 放射線物性Ⅰ、伊藤憲昭、森北出版株式会社、1981
- イオンビーム工学 - イオン・固体相互作用編、藤本文範・小牧研一郎 編、内田老鶴圃、1995
- イオンビームによる表面分析・物質改質、藤本文範・小牧研一郎 編、内田老鶴圃、2000
- Fundamental of Surface anf Thin Film Analysis, L. C. Feldman, J. W. Mayer (North-Holland, Amsterdam, 1986)
- Material Analysis by Ion Channeling, L. C. Feldman, J. W. Mayer, S. T. Picraux (Academic Press, NewYork, 1982)
- Backscattering Spectroscopy, W. K. Chu, J. W. Mayer, M. -A. Nicholet (Academic Press, NewYork, 1978)
- Ion Beams for Material Analysis, J. R. Bird, J. S. Williams eds. (Academic Press, Australia, 1989)
- Surface Analysis Methods in Material Science, D. J. O'Connor, B. A. Sexton, R. St. C. Smart eds. (Springer-Verlag, Berlin, 1992)
